Question

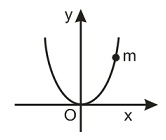
A bead of mass m is located on a parabolic wire with its axis vertical and vertex at the origin as shown in figure and whose equation is x² = 4ay. The wire frame is fixed and the bead can slide on it without friction. The bead is released from the point y = 4a on the wire frame from rest. The tangential acceleration of the bead when it reaches the position given by y = a is :

• A. $\frac{\text{g}}{2}$
• B. $\frac{\sqrt{3 \, } \text{g}}{2}$
• C. $\frac{\text{g}}{\sqrt{2}}$
• D. $\frac{\text{g}}{\sqrt{5}}$

Answer 1

Answer: (C)

x² = 4ay
Differentiating w.r.t. y, we get
$\frac{\text{dy}}{\text{dx}} = \frac{\text{x}}{2 \text{a} }$

$∴ \, \text{At} \left(2 \text{ a, a}\right) \text{,} \frac{\text{dy}}{\text{dx}} = 1 \, \, \, ⇒ \, $ hence $\theta = 4 5^{^\circ }$
the component of weight along tangential direction is mg sin $\theta $ .
hence tangential acceleration is $\text{g sin } \theta = \frac{\text{g}}{\sqrt{2}}$