Question

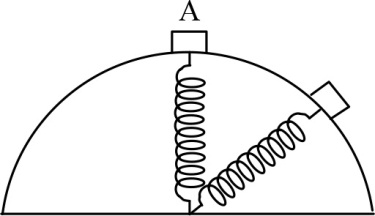
A bead of mass $m$ can slide without friction along a vertical ring of radius $R$ . One end of a spring of force constant $k=\frac{3 m g}{R}$ is connected to the bead and the other end is fixed at the centre of the ring. Initially, the bead is at the point $A$ and due to a small push it starts sliding down the ring. If the bead momentarily loses contact with the ring at the instant when the spring makes an angle of $60^\circ $ with the vertical, then the natural length of the spring is

• A. $\frac{5 R}{9}$
• B. $\frac{3 R}{4}$
• C. $\frac{5 R}{6}$
• D. $\frac{4 R}{7}$

Answer 1

Answer: (C)

Let's say the bead loses contact with the ring at point $B$ , then $N_{2}=0$ and
$mg \, cos60^\circ + \, kx=\frac{m v^{2}}{R}$
$\frac{m g}{2}+kx=\frac{m v^{2}}{R}$
Applying the conservation of mechanical energy principle between $A$ & $B$
$\frac{m v^{2}}{2}=mgR\left(1 - cos 60 ^\circ \right)=\frac{m g R}{2}$
$\Rightarrow \frac{m v^{2}}{R}=mg$
$\frac{m g}{2}+kx=mg$
$\Rightarrow x=\frac{m g}{2 k}=\frac{R}{6}$
The natural length of the spring $l=R-x=R-\frac{R}{6}=\frac{5 R}{6}$