Question

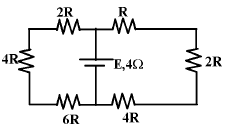
A battery of internal resistance $4 \, \Omega $ is connected to the network of resistances as shown in the figure. To deliver maximum power to the network, the magnitude of resistance $R$ (in $\Omega $ ) should be $\frac{\text{x}}{2 1}$ . Find $x$ .

• A. $16$
• B. $17$
• C. $19$
• D. $23$

Answer 1

Answer: (C)

The battery has an internal resistance of $4\Omega $ .
From maximum power transfer theorem, we know that for maximum power, the equivalent resistance of the network should be equal to the internal resistance of the battery.
$R_{eq}=4\Omega $
$\Rightarrow \frac{\left(7 \text{R}\right) \left(12 \text{R}\right)}{19 \text{R}}=\frac{84 \text{R}}{19}=4\Omega $
$\Rightarrow \text{R}=\frac{19}{21}\Omega $