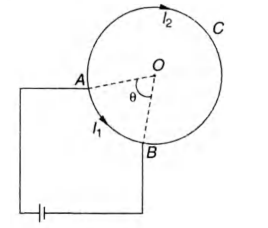
Question

A battery is connected between two points $A$ and $B$ on the circumference of a uniform conducting ring of radius $r$ and resistance $R$. One of the arcs $AB$ of the ring subtends an angle $\theta$ at the centre. The value of the magnetic induction at the centre due to the current in the ring is

• A. proportional to $(180^{\circ}-\theta)$
• B. inversely proportional to r
• C. zero, only if $(\theta=180^{\circ})$
• D. zero for all values of $\theta$

Answer 1

Answer: (D)

For a current flowing into a circular arc, the magnetic induction at the centre is
$B=\left(\frac{\mu_0 i}{4\pi r}\right)\theta$
or $B \propto i \theta$
In the given problem, the total current is divided into two arcs
$i \propto \frac{1}{\text{resistance of arc}} \propto \frac{1}{\text{length of arc} }$
$\propto \frac{1}{\text{angle subtended at centre}(\theta)}$
or $i\theta=$ constant
i.e. magnetic field at centre due to arc $AB$ is equal and opposite to the magnetic field at centre due to arc $ACB$. Or the net magnetic field at centre is zero.