Question

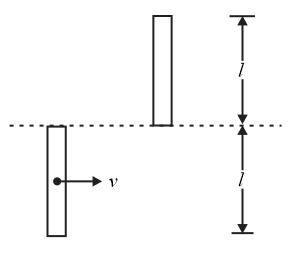
A bar of mass $m$ and length $l$ is in pure translational motion with its centre of mass moving with a velocity $v$ . It collides and sticks to another identical bar at rest as shown in the figure. Assuming that after the collision the system of the two bars becomes one composite bar of length $2l$ , then the angular velocity of the composite bar will be

• A. $\frac{3 v}{4 \textit{l}}$ , anti-clockwise
• B. $\frac{4 v}{3 \textit{l}}$ , anti-clockwise
• C. $\frac{3 v}{4 \textit{l}}$ , clockwise
• D. $\frac{4 v}{3 \textit{l}}$ , clockwise

Answer 1

Answer: (A)

By law of conservation of angular momentum
$\Sigma \mathrm{mvr}=\left(I_{\text {system }}\right) \omega$
$⇒ \, \text{mv} \frac{\textit{l}}{2} = \frac{\left(2 \text{m}\right) \left(2 \textit{l}\right)^{2}}{1 2} \omega = \frac{2 \text{m} \left(4 \left(\textit{l}\right)^{2}\right)}{1 2} \omega $
$⇒ \, \, \omega = \frac{3 \text{v}}{4 \textit{l}} \left(\text{anti-clockwise}\right)$
Note that clockwise or anti-clockwise rotation can only be determined here by the given diagram.