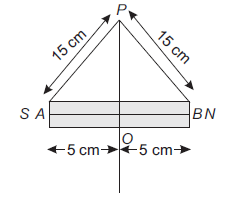
Question

A bar magnet is $10 cm$ long is kept with its north $(N)$ -pole pointing north. A neutral point is formed at a distance of $15 cm$ from each pole. Given the horizontal component of earth's field is $0.4$ Gauss, the pole strength of the magnet is

• A. 9 A - m
• B. 6.75 A - m
• C. 27 A - m
• D. 1.35 A - m

Answer 1

Answer: (B)

Length of magnet $=10 \,cm =10 \times 10^{-2} m $
$r=15 \times 10^{-2} m $

$O P=\sqrt{225-25}=\sqrt{200} \,cm$
Since, at the neutral point, magnetic field due to the magnet is equal to $B_{H}$
$B_{H}=\frac{\mu_{0}}{4 \pi} \cdot \frac{M}{\left(O P^{2}+A O^{2}\right)^{3 / 2}} $
$0.4 \times 10^{-4}=10^{-7} \times \frac{M}{\left(200 \times 10^{-4}+25 \times 10^{-4}\right)^{3 / 2}} $
$\frac{0.4 \times 10^{-4}}{10^{-7}} \times\left(225 \times 10^{-4}\right)^{3 / 2}=M $
$0.4 \times 10^{3} \times 10^{-6}(225)^{3 / 2}=M$
$M=1.35 \,A - m$