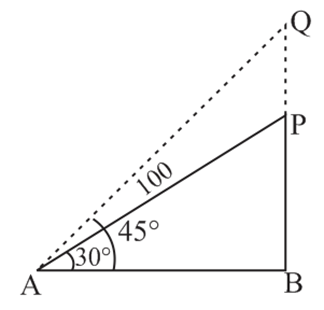
Question

A balloon is rising vertically upwards. At an instant, an observer on the ground, whose distance from the balloon is 100 meters, sees the balloon at an angle of elevation of $30^{\circ}$. If the balloon rises further vertically to a point where the angle of elevation as seen by the observer is $45^{\circ}$, then twice its height (in meters) from the ground is $($ Take $\sqrt{3}=1.73)$

Answer 1

Let $A$ be the observer, $P$ be the initial position of the balloon and it is at $Q$ when the angle of elevation is $45^{\circ}$
From triangle $A B P$ and triangle $A B Q$,
$\Rightarrow A B=50 \sqrt{3}=B Q$
and $B P=50$
So, $B Q=50(\sqrt{3})=50 \times 1.73$
$\Rightarrow B Q=86.5$ meters
$\Rightarrow 2 B Q=173$ $\Rightarrow 2BQ=173$