Question

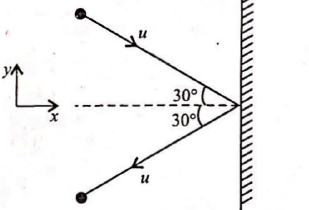
A ball of mass $m$ strikes a rigid wall with speed $u$ at an angle of $30^°$ and get reflected with the same speed and at the same angle as shown in the figure. If the ball is in contact with the wall for time $t,$ then the force acting on the wall is

• A. $\frac{mu \, sin\,30^{\circ}}{t}$
• B. $\frac{2 \,mu \, sin\,30^{\circ}}{t}$
• C. $\frac{mu\,cos\,30^{\circ}}{t}$
• D. $\frac{2\,mu\, cos\,30^{\circ}}{t}$

Answer 1

Answer: (D)

Initial momentum of the ball is
$\vec{p}_{i}$ $=mu \, cos \,30^{\circ} \hat{i}$ $-mu \, sin\,30^{\circ} \hat{j}$
Final momentum of the ball is
$\vec{p}_{f} $ $=-mu \,cos \, 30^{\circ} \hat{i}$ $-mu \, sin \, 30\, \hat{j}$
$\therefore \quad$ Change in momentum,
$\Delta\vec{p}$ $=\vec{p}_{f}$ $-\vec{p}_{i}$ $=-2 mu \, cos \, 30^{\circ} \hat{i}$
Impulse = Change in momentum $= -2 mu \, cos \, 30^{\circ} \hat{i}$
As impulse and force are in the same direction, therefore, force on the ball due to the wall is normal to the wall along the negative $x$-axis. Using Newton’s $3^{rd}$ law of motion the force on the wall due to the ball is normal to the wall along the positive $ x-$ direction.
$\therefore \quad$ $F=\frac{2\,mu\,cos\,30^{\circ}}{t}$