Question

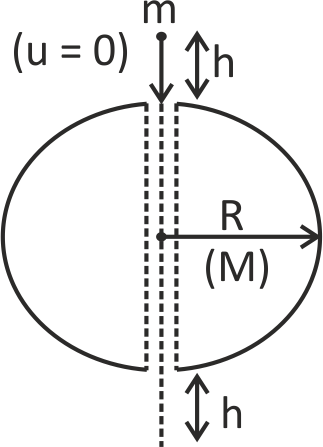
A ball of mass $m$ is dropped from a height $h$ in a tunnel, made across the earth (mass = $M$ , radius = $R$ ) passing through its centre. If $h$ such that the motion of the particle through $h$ can be considered uniformly accelerated at $g$ , then the time period of the particle is

• A. $2\pi \sqrt{\frac{R}{g}}+\sqrt{\frac{2 h}{g}}$
• B. $2\pi \sqrt{\frac{R}{g}}+2\sqrt{\frac{h}{g}}$
• C. $2\pi \sqrt{\frac{R}{g}}+4\sqrt{\frac{2 h}{g}}$
• D. $2\pi \sqrt{\frac{2 R}{g}}+\sqrt{\frac{h}{g}}$

Answer 1

Answer: (C)

The time, the particle takes to go through $h$ is
$t=\sqrt{\frac{2 h}{g}}$ and in one complete oscillation, the particle travels through $h$ four times.
For the motion of the particle through the tunnel, the force acting on the particle is towards the centre of the earth and it is proportional to the distance of the particle from the centre of the earth. Hence the motion of the particle through the tunnel will be like an SHM.
$F=-\frac{G M m}{R^{3}}x$
$a=-\frac{G M}{R^{3}}x$
$T_{SHM}=2\pi \sqrt{\frac{R^{3}}{G M}}=2\pi \sqrt{\frac{R}{g}}$
So the time period of the particle is
$T=T_{SHM}+4\sqrt{\frac{2 h}{g}}$
$T=2\pi \sqrt{\frac{R}{g}}+4\sqrt{\frac{2 h}{g}}$