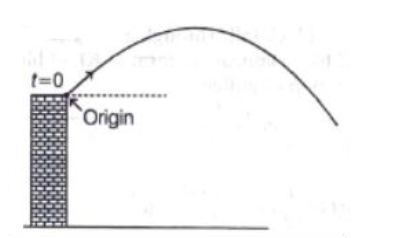
Question

A ball of mass $m=1\, Kg$ is thrown from the top of a building with initial velocity $\vec{v}=(20 \,m / s ) \hat{i}+(24 \,m / s ) \hat{j}$ at time $t =0\, s$. The change in the potential energy of the ball between $t=0$ and $t=6\, s$, if the ball does not hit the ground
(Assume $g =10\, m / s ^{2}$ )

• A. $-320 \,J$
• B. $-360 \,J$
• C. $-380 \,J$
• D. $+320\, J$

Answer 1

Answer: (B)

$u=20 \hat{i}+24 \hat{j}$

To find change in PE, we have to consider only vertical motion of the ball.
So, we have
$u_{y}=24 \,m / s , m=1 \,kg$
$a_{y}=-10 \,m / s ^{2}, t=6 \, s$
We take origin at point of projection,
$h =u_{y} t-\frac{1}{2} g t^{2}=24 \times 6-\frac{1}{2} \times 10 \times 36 $
$=144-180=-36 \,m$
So, vertical displacement of the particle is
$h=-36 \,m$
Hence, change in $P E=m g h$
$=1 \times 10 \times-36=-360 \, J$