Question

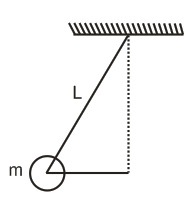
A ball of mass $m=0.5 \, kg$ is attached to the end of a string having length $L=0.5 \, m$ . The ball is rotated on a horizontal circular path about the vertical axis. The maximum tension that the string can bear is $324 \, N$ . The maximum possible value of the angular velocity of ball (in $rad \, s^{- 1}$ ) is

• A. $9$
• B. $18$
• C. $27$
• D. $36$

Answer 1

Answer: (D)

$\textit{T \, }\text{sin}\theta =m\omega ^{2}r$
$\textit{T \, }\text{sin}\theta =m\omega ^{2}L\text{sin}\theta $
$$
$\Rightarrow T=m\omega ^{2}L$
$\Rightarrow \, 324=\frac{1}{2}\left(\left(\omega \right)^{2}\right)\frac{1}{2}$
Therefore $\omega =36 \, rad \, s^{- 1}$