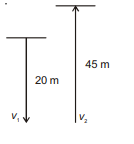
Question

A ball of mass $50\, g$ is dropped from a height of $20\, m$. A boy on the ground hits the ball vertically upwards with a bat with an average force of $200\, N$, so that it attains a vertical height of $45\, m$. The time for which the ball remains in contact with the bat is [Take $g=10\, m / s ^{2}$ ]

• A. $1 / 20^{\text {th }}$ of a second
• B. $1 / 40^{\text {th }}$ of a second
• C. $1 / 80^{\text {th }}$ of a second
• D. $1 / 120^{\text {th }}$ of a second

Answer 1

Answer: (C)

Using $v^{2}=u^{2}+2 a s$
$v_{1}=\sqrt{2 g(20)}=20\, m / s$
$v_{2}=\sqrt{2 g(45)}=30\, m / s$
Impulse $=F \Delta t=m\left(\vec{v}_{2}-\vec{v}_{1}\right)$
$\Rightarrow 200\, t=\frac{50}{1000}(20-(-30)$
$t=\frac{5}{400}=\frac{1}{80} s$