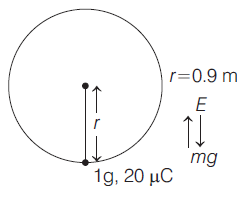
Question

A ball of mass $1 g$ having a charge of $20\, \mu C$ is tied to one end of a string of length $0.9 \,m$ can rotate in a vertical plane in a uniform electric field $100 \,NC ^{-1}$ directed upwards. The minimum horizontal velocity that must be given to the ball at the lowest position so that it completes the vertical circle is (Let, $g =10 \,ms ^{-2}$ )

• A. $9\, ms ^{-1}$
• B. $18\, ms ^{-1}$
• C. $36\, ms ^{-1}$
• D. $6\, ms ^{-1}$

Answer 1

Answer: (D)

Given, mass of ball, $m=1 \,g =\frac{1}{10^{3}} \,kg$
charge on the ball, $q=20 \,\mu C=20 \times 10^{-6} C$,
length of the string centre of one end, $r=0.9\, m$
electric field, $E=100\,N / C$
and acceleration due to gravity, $g=10 \,m / s ^{2}$
Now, according to the question, force exerted by the electric field due to charge on ball is given as, $\therefore $ Force $=$ Charge on the ball $\times$ Electric field
$F =q E \Rightarrow F=20 \times 10^{-6} \times 100 $
$F_{1} =2 \times 10^{-3} \,N$
Now, force due to the gravitation,
$F_{2}=m g=\frac{1}{10^{3}} \times 10=10 \times 10^{-3} \,N$
Net effective force on the ball,
$F_{e f f}=F_{2}-F_{1}$
From Eqs. (ii) and (i), we get
$F_{\text {eff }}=10 \times 10^{-3}-2 \times 10^{-3} \Rightarrow f_{\text {eff }}=8 \times 10^{-3} N$
Now, effective gravitational acceleration at lowest position is given as,
$F_{e f f}=m g_{\text {eff }}$
$g_{\text {eff }}=\frac{F_{\text {eff }}}{m}=\frac{8 \times 10^{-3}}{10^{-3}}=8 m / s ^{2}$
The minimum horizontal velocity that mut be given to the ball at the lowest position is,
$v=\sqrt{5 g_{\text {eff }} r} \Rightarrow v=\sqrt{5 \times 8 \times \frac{9}{10}}$
$v=\sqrt{4 \times 9}=\sqrt{36} \Rightarrow v=6 \,m / s$