Question

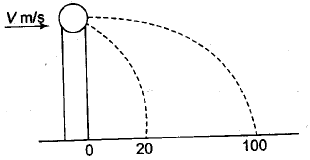
A ball of mass $0.2 \, kg$ rests on a vertical post of height $5 \, m$ . A bullet of mass $0.01 \, kg$ , travelling with a velocity $V \, m \, s^{- 1}$ in a horizontal direction, hits the centre of the ball. After the collision, the ball and bullet travel independently. The ball hits the ground at a distance of $20 \, m$ and the bullet at a distance of 100 m from the foot of the post. The velocity $V$ of the bullet is

• A. $250ms^{- 1}$
• B. $350 \, m \, s^{- 1}$
• C. $400 \, m \, s^{- 1}$
• D. $500 \, m \, s^{- 1}$

Answer 1

Answer: (D)

Time of flight $\left(t_{f}\right)=\sqrt{\frac{2 h}{g}}=\sqrt{\frac{2 \times 5}{10}}=1s$
Horizontal range (R) = horizontal velocity $\times $ time of flight
$\therefore $ Horizontal velocities of the bullet and of the ball after the collision respectively are
$\left(v\right)_{b u l l e t}=\frac{100}{1}=100 \, ms^{- 1}$
$\left(v\right)_{b a l l}=\frac{20}{1}=20 \, ms^{- 1}$
From the conservation of momentum, Total initial momentum = total final momentum
$\Rightarrow \left(m\right)_{b u l l e t}\times V=\left(m\right)_{b u l l e t}\times \left(v\right)_{b u l l e t}+\left(m\right)_{b a l l}\times \left(v\right)_{b a l l}$
$\Rightarrow 0.01 \, V=0.01 \, \times 100+0.2\times 20$
$\Rightarrow V=500 \, ms^{- 1}$