Question

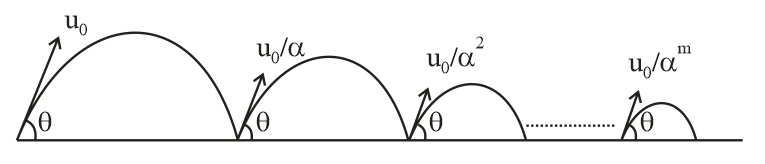
A ball is thrown from ground at an angle $\theta $ with horizontal and with an initial speed $u_{0}.$ For the resulting projectile motion, the magnitude of average velocity of the ball up to the point when it hits the ground for the first time is $V_{1}.$ After hitting the ground, the ball rebounds at the same angle $\theta $ but with a reduced speed of $u_{0}/\alpha .$ Its motion continues for a long time as shown in figure. If the magnitude of average velocity of the ball for entire duration of motion is $0.8V_{1},.$ the value of $\alpha $ is

Answer 1

$V_{\text{avg }}=\frac{R_{1} + R_{2} + R_{3} + \ldots \ldots }{T_{1} + T_{2} + T_{3} + \ldots \ldots }$
$V_{avg}=\frac{\frac{2 u_{x_{1}} u_{y_{1}}}{g} + \frac{2 u_{x_{2}} u_{y_{2}}}{g} + \ldots .}{\frac{2 u_{y_{1}}}{g} + \frac{2 u_{y_{2}}}{g} + \ldots . .}$
$=\frac{u_{0} cos \theta \cdot u_{0} sin \theta + \frac{u_{0}}{\alpha } cos \theta \cdot \frac{u_{0}}{\alpha } sin \theta + \ldots .}{u_{0} sin \theta + \frac{u_{0}}{\alpha } sin \theta + \frac{u_{0}}{\alpha ^{2}} sin \theta + \ldots .}$
$=\frac{u_{0} cos \theta \left[1 + \frac{1}{\alpha ^{2}} + \frac{1}{\alpha ^{4}} + \ldots \cdot \frac{1}{\alpha ^{2 n}}\right]}{\left[1 + \frac{1}{\alpha } + \frac{1}{\alpha ^{2}} + \ldots \ldots + \frac{1}{\alpha ^{n}}\right]}$
Given, $u_{0}cos\theta =V_{1}$
$\&V_{avg}=0.8v_{1}$
$0.8v_{1}=\frac{v_{1} \left[1 + \frac{1}{\alpha ^{2}} + \frac{1}{\alpha ^{4}} + \ldots . . + \frac{1}{\alpha ^{2 n}}\right]}{1 + \frac{1}{\alpha } + \frac{1}{\alpha ^{2}} + \ldots . + \frac{1}{\alpha ^{n}}}$
$0.8=\frac{\left[\frac{1}{1 - \frac{1}{\alpha ^{2}}}\right]}{\left[\frac{1}{1 - \frac{1}{\alpha }}\right]}$
$=\frac{\frac{1}{\left(1 - \frac{1}{\alpha }\right) \left(1 + \frac{1}{\alpha }\right)}}{\frac{1}{\left(1 - \frac{1}{\alpha }\right)}}$
$0.8=\frac{1}{\left(1 + \frac{1}{\alpha }\right)}$
$1+\frac{1}{\alpha }=\frac{1}{0 . 8}$
$\frac{1}{\alpha }=\frac{10}{8}-1$
$\frac{1}{\alpha }=\frac{2}{8}$
$\alpha =\frac{8}{2}=4$