Q.
A ball is projected from the point $O$ with velocity $20 \,m / s$ at an angle of $60^{\circ}$ with horizontal as shown in the figure. At highest point of its trajectory, it strikes a smooth plane of inclination $30^{\circ}$ at point $A$. The collision is perfectly inelastic. The maximum height from the ground attained by the ball is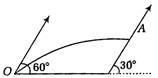
ManipalManipal 2015
Solution:
