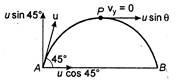
Q. A ball is hit at $ 45{}^\circ $ to the horizontal with a kinetic energy $ {{E}_{k}} $ . The kinetic energy at the highest point is
JamiaJamia 2006
Solution:
Key Idea: At the highest point vertical component of velocity is zero. Kinetic energy is possessed due to velocity. If m is mass of ball, then kinetic energy is
$ {{E}_{k}}=\frac{1}{2}m{{u}^{2}} $ At the highest point or path only horizontal component of velocity exists, hence kinetic energy is, $ E{{}_{k}}=\frac{1}{2}m{{(u\cos 45{}^\circ )}^{2}}=\frac{1}{2}m{{\left( \frac{u}{\sqrt{2}} \right)}^{2}} $ $ \therefore $ $ E{{}_{k}}=\frac{1}{2}\left( \frac{1}{2}m{{u}^{2}} \right)=\frac{{{E}_{k}}}{2} $