Q.
$A B$ is an inclined plane of inclination $30^{\circ}$ with horizontal. Point $O$ is $20\, m$ above point $A$. A particle is projected horizontally from $O$ leftwards, and it collides with the plane $A B$ perpendicularly. Speed of the particle at the time of projection should be $\left(g=10 \,m / s ^{2}\right)$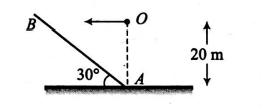
Motion in a Plane
Solution:
