Q.
$A B C D$ is the plane of glass cube. A horizontal beam of light enters the face $A B$ at the grazing incidence. Show that the angle $\theta$ which any ray emerging from $B C$ would make with the normal to $B C$ is given by $\sin \theta=\cot \alpha$ where $\alpha$ is the critical angle. The greatest value that the refractive index of glass may have if any of the light is to emerge from $B C$ is $\sqrt{a}$, then value of $a$ is ?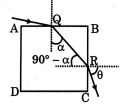
Ray Optics and Optical Instruments
Solution:
