Q.
$A B$ and $C D$ are two identical rods each of length $l$ and mass $m$ joined to form a cross. The moment of inertia of these two rods about a bisector $(X Y)$ of angle between the rods is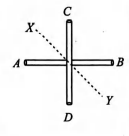
System of Particles and Rotational Motion
Solution:
