Q.
$A$ and $B$ are two points on a uniform ring of resistance $15\,\Omega$. The $\angle AOB = 45^{\circ}$. The equivalent resistance between $A$ and $B$ is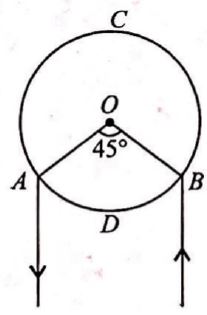
Current Electricity
Solution:

Solution: