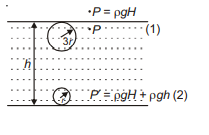
Q. A air bubble rises from bottom of a lake to surface. If its radius increases by $200 \%$ and atmospheric pressure is equal to water coloumn of height $H_{1}$ then depth of lake is
Mechanical Properties of Fluids
Solution:
Let initial radius be $=r$
Final radius $=r+200 \%$ of $r$
$=3 r$
Atmospheric pressure $=\rho g H$
Let depth of the lake be $h$
So, pressure at the bottom of lake $=\rho g H+\rho g h$
Using $P_{1} V_{1}=P_{2} V_{2}$
$\rho g H \times \frac{4}{3} \pi(3 r)^{3}=(\rho g H+\rho g h) \times \frac{4}{3} \pi r^{3}$
$\rho g H \times \frac{4}{3} \pi \times 27 r^{3}=(\rho g H) \frac{4}{3} \pi r^{3}+\rho g h \times \frac{4}{3} \pi r^{3}$
Solving this equation we get
$26\, H=h$