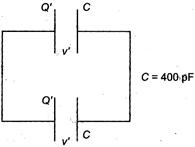
Q. A $ 400\,pF $ capacitor is charged by a $ 100\,V $ supply. How much electrostatic energy is lost in the process of disconnecting from the supply and connecting another uncharged $ 400\,pF $ capacitor?
J & K CETJ & K CET 2014Electrostatic Potential and Capacitance
Solution:
$C=400 \times 10^{-12} F$
$V=100\, V$
Initially energy stored $=\frac{1}{2} C V^{2}$
$=\frac{1}{2} 400 \times 10^{-12} \times\left(10^{2}\right)^{2}$
$=\frac{1}{2} \times 4 \times 10^{-10} \times 10^{4}$
$=2 \times 10^{-6} J$
$\Rightarrow Q=C V=4 \times 10^{-10} \times 100$
$=4 \times 10^{-8} C$
$\Rightarrow $ By again connecting the charged capacitor with a uncharged ideal capacitor.
$\Rightarrow $ Now, the charge $Q$ will divide into two capacitors.
$\Rightarrow $ As $V$ and $C$ are same for both, $Q'$ will be same for both,
$\Rightarrow $ So $Q'=\frac{Q}{2}=2 \times 10^{-8} C$
$\Rightarrow $ So, energy stored in both the capacitors $=\left(\frac{\left(Q'\right)^{2}}{2 C}\right)=\frac{\left(Q'\right)^{2}}{2 C}$
$=\frac{\left(2 \times 10^{-8}\right)}{8 \times 10^{-10}}=10^{-6} J$
So energy lost $=2 \times 10^{-6}-0.25 \times 10^{-6}$
$=0.75 \times 10^{-6} J \approx 10^{-6} J$