Question

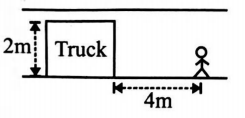
$A\, 2$ m wide truck is moving with a uniform speed of $8\, m/s$ along a straight horizontal road. A pedestrian starts crossing the road at an instant when the truck is $4\, m$ away from him. The minimum constant velocity with which he should run to avoid an accident is :

• A. $1.6 \sqrt{5} m / s$
• B. $1.2 \sqrt{5} m / s$
• C. $1.2 \sqrt{7} m / s$
• D. $1.6 \sqrt{7} m / s$

Answer 1

Answer: (A)

$( v \sin \theta) t =2$
$(8-v \cos \theta) t=4$
$\frac{v \sin \theta}{8-v \cos \theta}=\frac{1}{2}$
$2 v \sin \theta=8-v \cos \theta$
$2 v \sin \theta+v \cos \theta=8$
$v =\frac{8}{2 \sin \theta+\cos \theta}$
$v _{\min }=\frac{8}{\sqrt{2^{2}+1^{2}}}$
$v _{\min }=\frac{8}{\sqrt{5}}$
$=\frac{8 \sqrt{5}}{\sqrt{5} \sqrt{5}}$
$=1.6 \sqrt{5}$