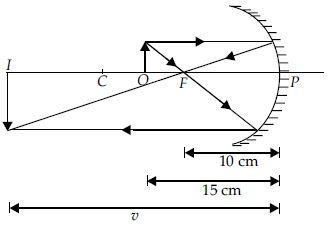
Q. A $2.0\, cm$ tall object is placed $15\, cm$ in front of a concave mirror of focal length $10\, cm$. What is the size and nature of the image?
Solution:
According to new cartesian sign convention, Object distance, u = -15 cm
Focal length of the concave mirror, f = -10 cm Height of the object, $h_O = 2$ cm
According to mirror formula, $\frac{1}{v}+\frac{1}{u}=\frac{1}{f}$
$\Rightarrow \quad \frac{1}{v}=\frac{1}{f}-\frac{1}{u}=\frac{1}{-10}-\frac{1}{-15}=\frac{1}{-10}+\frac{1}{15}$
or $\quad v = -30$ cm.
The image is formed at a distance of 30 cmfrom the mirror on the same side of the object.It is a real image.
Magnification of the mirror, $m=\frac{-v}{u}=\frac{h_{1}}{h_{0}}$
$\Rightarrow \quad\frac{-\left(-30\right)}{-15}=\frac{h_{I}}{2}\quad\Rightarrow \quad h_{1}=-4$ cm.
Negative sign shows that image is inverted. The image is real, inverted, of size 4 cm at a distance of 30 cm in front of the mirror.