Question

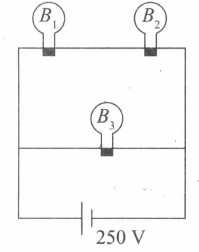
A $100\,W$ bulb $B_{1}$ and two $60\,W$ bulbs $B_{2}$ and $B_{3}$ are connected to a $250\,V$ source as shown in the figure. Now $W_{1},W_{2}$ and $W_{3}$ are the output powers of the bulbs $B_{1},B_{2}$ and $B_{3}$ respectively. Then

• A. $W_{1}>W_{2}=W_{3}$
• B. $W_{1}>W_{2}>W_{3}$
• C. $W_{1} < W_{2}=W_{3}$
• D. $W_{1} < W_{2} < W_{3}$

Answer 1

Answer: (D)

Let suppose the resistance of bulb $B_{1 },B_{2}$ and $B_{3}$ are $R_{1},R_{2}$ and $R_{3}$ respectively.
Now by using the formula of power $P=\frac{V^{2}}{R}$ , We can write $R_{1}=\frac{V^{2}}{100},$ $R_{2}=\frac{V^{2}}{60}$ and $R_{3}=\frac{V^{2}}{60}$ .
Let us suppose that current through series combination of $B_{1}$ and $B_{2}$ is $I$ and current through $B_{3}$ is $I^{'}$ .
Now by using current division law we can write $I=\frac{ER_{3}}{R_{1} + R_{2} + R_{3}}$ and $I^{'}=\frac{E \left(R_{1} + R_{2}\right)}{R_{1} + R_{2} + R_{3}}$ where $E=250V$
Output power, $W=I^{2}R$
Hence $W_{1}˸W_{2}˸W_{3}=I^{2}R_{1}˸I^{2}R_{2}˸\left(I^{'}\right)^{2}R_{3}$ $\Rightarrow W_{1}˸W_{2}˸W_{3}=\frac{E^{2} \left(R_{3}\right)^{2}}{\left(R_{1} + R_{2} + R_{3}\right)^{2}}R_{1}˸\frac{E^{2} \left(R_{3}\right)^{2}}{\left(R_{1} + R_{2} + R_{3}\right)^{2}}R_{2}˸\frac{E^{2} \left(R_{1} + R_{2}\right)^{2}}{\left(R_{1} + R_{2} + R_{3}\right)^{2}}R_{3}$
$\Rightarrow W_{1}˸W_{2}˸W_{3}=R_{3}R_{1}˸R_{3}R_{2}˸\left(R_{1} + R_{2}\right)^{2}$
$\Rightarrow W_{1}˸W_{2}˸W_{3}=\left(\frac{V^{2}}{60} \times \frac{V^{2}}{100}\right)˸\left(\frac{V^{2}}{60} \times \frac{V^{2}}{60}\right)˸\left(\frac{V^{2}}{100} + \frac{V^{2}}{60}\right)^{2}$
$\Rightarrow W_{1}:W_{2}:W_{3}=0.0001:0.0002:0.0007$
$\Rightarrow W_{1} < W_{2} < W_{3}$