Q.
A $100\, V, AC$ source of frequency $500\, Hz$ is connected to an LCR circuit with $ L=8.1\,mH, $ $ C=12.5\mu F,R=10\,\Omega $ all connected in series as shown in figure. What is the quality factor of circuit?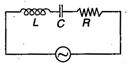
Bihar CECEBihar CECE 2008Alternating Current
Solution: