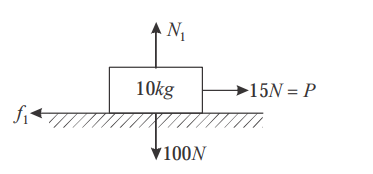
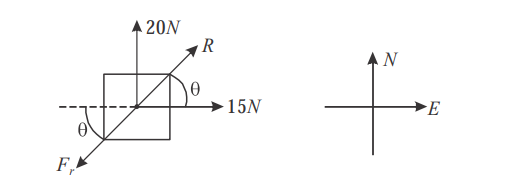
Question

A $10\, kg$ block is placed on a horizontal surface whose coefficient of friction is $0.2$. A horizontal force $P=15 \, N$ first acts on it in the eastward direction. Later, in addition to $P$ a second horizontal force $Q=20\, N$ acts on it in the northward direction : (Take $g=10 \, m / s ^{2}$ )

• A. The block will not move when only $P$ acts, but will move when both $P$ and $Q$ act
• B. If the block moves, the acceleration will be $0.5 \, m / s ^{2}$
• C. When the block moves, its direction of motion will be $\tan ^{-1}(13 / 4)$ east of north
• D. When both $P$ and $Q$ act, the direction of the force of friction acting on the block will be $\tan ^{-1}(3 / 4)$ west of south

Answer 1

Answer: (A), (B), (C)

$f_{1 \max } =0.2 \times 10 \times 10 $
$=20\,N$
As $f_{1 \max }< P$, friction force
$f_{1}=15\, N $ and block do not move
When both $P$ and $Q$ acts, resultant applied force,
$R =\sqrt{P^{2}+Q^{2}}=\sqrt{15^{2}+20^{2}}$
$=\sqrt{625}=25 N$
$R >f_{1 \text { max }}$, thus block moves when both $P$ and $Q$ acts
$a=\frac{R-f_{1 \max }}{m} $
$=\frac{25-20}{10}=\frac{5}{10}=0.5\, m / s ^{2}$
Direction of $\vec{R}$,
$ \tan \theta =\frac{15}{20}=\frac{3}{4} $
$ \theta =\tan ^{-1} \frac{3}{4} $ (east of north)

Thus, direction of force of friction $\left(F_{r}\right)$ will be opposite to $R$, i.e. west of south.