Question

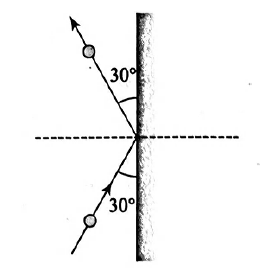
A $0.5\, kg$ ball moving with a speed of $12\, m/s$ strikes a hard wall at an angle of $30^{\circ}$ with the wall. It is reflected with the same speed and at the same angle. If the ball is in contact with the wall for $0.25\, s,$ the average force acting on the wall is

• A. 48 N
• B. 24 N
• C. 12 N
• D. 96 N

Answer 1

Answer: (B)

The vector $O \vec{A}$ represents the momentum of the object before the collision, and the vector $O \vec{B}$ that after the collision.
The vector $\vec{A} B$ represents the change in momentum of the object $\Delta \vec{P}$.
As the magnitudes of $O \vec{A}$ and $O \vec{B}$ are equal, the components of $O \vec{A}$ and $O \vec{B}$ along the wall are equal and in the same direction, while those perpendicular to the wall are equal and opposite.
Thus, the change in momentum is due only to the change in direction of the perpendicular components.
Hence, $\Delta p =O B \sin 30^{\circ}-\left(-O A \sin 30^{\circ}\right)$
$=m v \sin 30^{\circ}-\left(-m v \sin 30^{\circ}\right)$
$=2 m v \sin 30^{\circ}$

Its time rate will appear in the form of average force acting on the wall.
$F \times t=2 m v \sin 30^{\circ}$
Or $F=\frac{2 m v \sin 30^{\circ}}{t}$
Given, $m =0.5\, kg ,\, v=12\, m / s,\, t=0.25\, s$
$\theta =30^{\circ}$
Hence, $F =\frac{2 \times 0.5 \times 12 \sin 30^{\circ}}{0.25}$
$=24\, N$