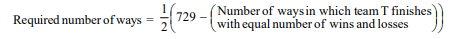Question

6 In a football tournament a team T has to play with each of the 6 other teams once. Each match can result in a wins, draw or loss. Find the number of ways in which the team T finishes with more wins than losses

Answer 1

Total ways $=3^6=729 \times \times \times \times \times \times$

Now, we shall consider following cases.
Case-1: 0 draw, 3 wins and 3 loss: W W W L L L $=\frac{6 !}{3 ! 3 !}={ }^6 C _3=20$
Case-2: 1 win, 1 loss, 4 draw : W L D D D D $=\frac{6 !}{4 !}=30$
Case -3: 2 win, 2 loss, 2 draw : $ W$ W L L D D $=\frac{6 !}{2 ! 2 ! 2 !}=90$
Total ways with equal wins and draws $=20+30+90+1=141$
So, required number of ways $=\frac{1}{2}(729-141)=\frac{588}{2}=294$.