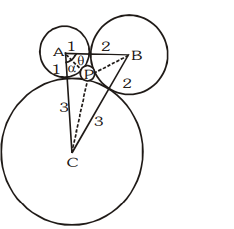
Question

$3$ circle of radii $1,2$ and $3$ and centres at $A , B$ and $C$ respectively, touch each other. Another circle whose centre is $P$ touches all these 3 circles externally and has radius $r$. Also $\angle PAB =\theta$ & $\angle PAC =\alpha$ -

• A. $\cos \theta=\frac{3-r}{3(1+r)}$
• B. $\cos \alpha=\frac{2-r}{2(1+r)}$
• C. $r=\frac{6}{23}$
• D. $r=\frac{6}{\sqrt{23}}$

Answer 1

Answer: (A), (B), (C)

$\triangle ABC$ is right angle
Applying cosine rule in $\triangle PAB$
$\cos \theta=\frac{3^2+(1+r)^2-(2+r)^2}{2 \cdot 3(1+r)}$
$=\frac{3-r}{3(1+r)}$
Again applying cosine rule in $\triangle PAC$
$\cos \alpha=\frac{(1+r)^2+4^2-(3+r)^2}{2 \cdot 4(1+r)}=\frac{2-r}{2(1+r)} $
$\because \alpha+\theta=90$
$\alpha=90-\theta \Rightarrow \cos \alpha=\sin \theta $
$\left(\frac{3-r}{3(r+1)}\right)^2+\left(\frac{2-r}{2(r+1)}\right)^2=1$