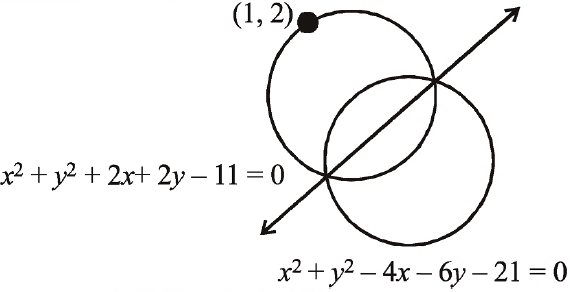Question

The equation of the circle passing through the point (1,2) and through the points of intersection of $x^2+y^2-4x-6y-21=0$ and $3x+4y+5=0$ is given by

• A. $x^2+y^2+2x+2y+11=0$
• B. $x^2+y^2-2x+2y-7=0$
• C. $x^2+y^2+2x-2y-3=0$
• D. $x^2+y^2+2x+2y—11=0$

Answer 1

Answer: (D)

Point $(1,2)$ lies on the circle $x^2+y^2+2x+2y-11=0$, because coordinates of point $(1,2)$ satisfy the equation
$x^2+y^2+2x+2y-11=0$
Now, $x^2+y^2-4x-6y-21=0...(i)$
$x^2+y^2+2x+2y-11=0...(ii)$
$3jc+4y+5=0...(iii)$
From (i) and (iii).
$x^2+{\left(\frac{3x+5}{4}\right)}^2-4x-6\left(-\frac{3x+5}{4}\right)-21=0$
$\Rightarrow 16x^2+9x^2+30x+25-64x+72x+120-336=0$
$\Rightarrow 25x^2+38x-191=0\left(iv\right)$
From (ii) and (iii),
$x^2+{\left(-\frac{3x+5}{4}\right)}^2+2x+2\left(-\frac{3x+5}{4}\right)-11=0$
$\Rightarrow 16x^2+9x^2+30x+25+32x-24x-40-176=0$
$\Rightarrow 25x^2+38x-191=0\left(v\right)$
Thus we get the same equation from (ii) and (iii) as we get from equation (i) and (iii). Hence the point of intersections of (ii) and (iii) will be same as the point of intersections of (i) and (iii). Therefore the circle (ii) passing through the point of intersection of circle(i) and point (1,2) also as shown in the figure.
Hence equation(ii) i.e.
$x^2+y^2+2x+2y-11=0$ is the equation of required circle.